เซต เป็นคำที่ไม่ให้ให้นิยาม (Undefined Term) เรามักใช้เซตแทนสิ่งที่อยู่ร่วมกัน ซึ่งหมายถึงกลุ่มของสิ่งต่างๆ ที่เราสามารถกำหนดสมาชิกได้ชัดเจน (Well-Defined) หรือก็คือความหมายของเซตนั่นเอง
การเขียนเซต
1. เขียนแบบแจกแจงสมาชิก (Tabular Form) เป็นการเขียนเซตโดยบรรจุสมาชิกทั้งหมดของเซตลงในวงเล็บปีกกา และระหว่างสมาชิกแต่ละตัวคั่นด้วยเครื่องหมายจุลภาค (,)
เช่น {A,B,C} หรือ {1, 2, 3} เป็นต้น
(หมายเหตุ: ถ้าเซตมีจำนวนสมาชิกมากมาย เราใช้ “…” แทนสมาชิกที่เหลือ)
2. เขียนสับเซตแบบบอกเงื่อนไขของสมาชิกในสับเซต (Set builder form)
มีหลักการ คือ แทนสมาชิกของเซตด้วยตัวแปรแล้วกำหนดเงื่อนไขเกี่ยวกับตัวแปรนั้น เพื่อแสดงว่ามีสิ่งใดบ้างที่เป็นสมาชิกของเซต
วิธีเขียนเซตโดยวิธีนี้ คือ เขียนตัวแปรและสิ่งที่กำหนดเงื่อนไขเกี่ยวกับตัวแปรลงในวงเล็บปีกกาและคั้นตัวแปรกับสิ่งที่กำหนดเงื่อนไขเกี่ยวกับตัวแปรด้วยเครื่องหมาย “|” หรือ “:”
3. การเขียนเซตด้วยวิธีอื่นๆ เช่น แบบบรรยาย, แบบใช้แผนภาพเวนน์, แบบช่วง เป็นต้น
แผนภาพเวนน์-ออยเลอร์ เป็นแผนภาพที่ใช้เขียนแทนเซตซึ่งแทนเอกภพสัมพัทธ์ U ด้วยสี่เหลี่ยมผืนผ้า และแทนเซต A, B, … ด้วยรูปวงกลม หรือวงรี หรือรูปปิดอื่นๆ ดังรูป
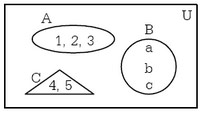
ซึ่งในเรื่องของแผนภาพนี้เรายังทำไปประยุกต์ใช้ในเรื่องการกระทำระหว่างเซต ซึ่งแสดงด้วยแผนภาพจะทำให้ดูเข้าใจง่ายขึ้น
สามารถดูเนื้อหาในนี้ได้เลยค่ะ คลิกอ่านได้เลยค่ะ
เนื้อหาคณิตศาสตร์ ม.4 เรื่องเซต
- ความหมายของเซต
- เซตจำกัด และเซตอนันต์
- เซตว่าง และเอกภพสัมพัทธ์
- ยูเนียน อินเตอร์เซกชันและคอมพลีเมนต์ของเซต
- สับเซตและเพาเวอร์เซต
- แผนภาพเวนน์-ออยเลอร์


ไม่มีความคิดเห็น:
แสดงความคิดเห็น